-
Por que é necessário conta em mais de uma casa de apostas? Para maximizar o seu +EV!

1. Maximização do Valor Esperado
O Valor Esperado é calculado como:EV=(Probabilidade×LucroPotencial)−(ProbabilidadedoEventoNa~oAcontecer×Custo)EV = (Probabilidade \times Lucro Potencial) – (Probabilidade do Evento Não Acontecer \times Custo)EV=(Probabilidade×LucroPotencial)−(ProbabilidadedoEventoNa~oAcontecer×Custo)
Ao conseguir melhores cotações, o lucro potencial aumenta, o que pode transformar apostas marginais ou negativas (EV negativo) em apostas positivas (EV positivo), ou tornar o EV positivo ainda maior.
2. Diferenças de Cotações
As casas de apostas oferecem cotações diferentes porque ajustam seus modelos com base em:
- Volume de apostas.
- Análises internas.
- Margens específicas.
Diferenças de cotações podem ser significativas o suficiente para impactar a lucratividade no longo prazo. Por exemplo:
- Casa A oferece uma cotação de 1.90.
- Casa B oferece 2.10 para o mesmo evento. Nesse caso, a cotação de 2.10 oferece maior retorno potencial com o mesmo risco, aumentando o EV.
3. Redução das Margens das Casas
Ao escolher sempre as melhores cotações, você está, na prática, “forçando” uma redução na margem das casas de apostas. Isso acontece porque você está aproveitando o mercado mais competitivo disponível.
4. Arbitragem e “Sure Bets”
Ter contas em várias casas também possibilita encontrar situações de arbitragem, onde as discrepâncias de cotações permitem lucro garantido, independentemente do resultado. Isso é especialmente valioso em mercados com alta liquidez e variações rápidas.
5. Flexibilidade Estratégica
Ao diversificar entre casas de apostas, você pode:
- Evitar limites prematuros: Apostar sempre na mesma casa pode levar a limitações na sua conta se você demonstrar ser um apostador lucrativo.
- Aproveitar promoções: Muitas casas oferecem bônus, “odds boost” ou cashback, o que pode melhorar ainda mais o EV de suas apostas.
Conclusão
Ter contas em várias casas de apostas é uma estratégia inteligente para maximizar o Valor Esperado e aumentar suas chances de lucrar no longo prazo. Isso requer pesquisa constante das cotações disponíveis e disciplina para sempre apostar naquelas que oferecem as melhores condições.
-
O fumo entrou. Devo procurar emprego?

Sabemos que estamos passando por uma fase difícil, mas é nessas horas que a disciplina e a gestão de banca se tornam ainda mais cruciais. Precisamos lembrar que apostas esportivas não são uma maratona de curto prazo, mas um jogo de resistência, onde quem sobrevive são os que mantêm a calma e a estratégia. A gestão de banca é o pilar fundamental para o sucesso a longo prazo. Sem ela, qualquer sequência ruim pode nos levar a perdas irreparáveis.
Devemos evitar ao máximo as apostas por impulsão. Quando estamos frustrados, a tentação de “recuperar” o que foi perdido em uma única aposta é grande, mas isso pode nos colocar em um buraco ainda maior. Cada aposta deve ser feita com a cabeça fria e baseada em análise, não em emoção. É importante lembrar que o controle emocional é tão vital quanto a análise técnica.
Portanto, vamos manter a disciplina, seguir o plano e respeitar a gestão de banca. Apostar com responsabilidade é a chave para atravessar essa fase e alcançar a estabilidade que buscamos. Juntos, com paciência e foco, vamos superar esse momento. Lembre-se, o jogo é longo e a vitória é dos que sabem esperar.
-
Como devo dividir meu dinheiro entre as casas?! Use o seu banco!

A triade | +EV bets trabalha com gestão de 200u até então. Como devo dividir esse dinheiro entre as casas de aposta?!
Nossa casa de maior volume é a Bet365, logo a maior parte da sua banca deve estar lá.
O ideal seria:
Bet365 – 60% da banca
Novibet – 15% da banca
Superbet – 10% da banca
Betano – 15% da bancaApesar da Betano não estar sendo muito utilizada, ela será essencial pra volta da NBA. Mas a dica do post não é essa e sim:
Tenha uma parte da sua banca no BANCO! É comum encontrarmos oportunidades muito boas em outras casas de aposta, como a Betfair, Sportingbet, Sportsbet, entre outras.
Pra agilizar o trâmite, o ideal é ter uma parte da sua banca no BANCO.
Isso além de agilizar o processo, te traz muito mais segurança em relação a seu dinheiro. -
O perigo de uma sequência de lucros absurda

E aí, galera das apostas! Bora bater um papo sério sobre essa coisa de sequência de vitórias? Eu sei, é tentador pensar que estamos no topo do mundo quando nossas apostas estão rendendo só vitórias, uma atrás da outra. Mas sério, vou te contar um segredo que pode salvar sua banca: isso pode ser perigoso demais!
É tipo uma montanha-russa, né? A adrenalina vai lá em cima quando você tá ganhando tudo, mas, meu amigo, a queda pode ser feia. Às vezes, a gente se empolga tanto com as vitórias que esquece que o jogo pode virar a qualquer momento.
Aqui vai uma dica de ouro: paciência é sua melhor amiga nessa jornada de apostas. Eu sei que é difícil segurar a ansiedade quando tá tudo indo bem, mas lembre-se de que uma maré de vitórias não dura pra sempre.
E não podemos esquecer da gestão de banca, mano! Isso é essencial. É tipo o alicerce da sua casa de apostas. Sem uma boa gestão de banca, você tá jogando com fogo. Por mais tentador que seja aumentar as apostas quando tá ganhando, é melhor seguir o plano, doa a quem doer.
Aqui vão as dicas de ouro pra você iniciante SÓ ganhar dinheiro a longo prazo:
– Não aumente sua stake no meio de um mês
– Faça sempre a gestão adequada conforme recomendamos: Divida sua banca em 150u
– Aposte SOMENTE naquilo que for enviado no grupo
– Use as apostas grátis que as casas te dão pra se divertir, montar seus bingos & loucuras!Ah, e outra coisa importante: respeita o tipster, pô! Se você tá seguindo alguém que você confia, não adianta nada ficar mudando as coisas só porque tá ganhando ou perdendo. Confiança é chave nesse jogo.
Então, galera, fica aí o recado: curta suas vitórias, claro, mas não deixe a empolgação te cegar. Mantenha a paciência, respeite a gestão de banca e siga firme no plano do tipster. Assim, você tá muito mais preparado pra qualquer montanha-russa que o mundo das apostas te jogar.
Bons green, e até a próxima!
– Yan Arruda -
Gestão de Banca – Qual a melhor forma de gerir uma banca?
Gestão de banca nas apostas e consciência da variância são competências essenciais dos apostadores. Qual é a relação entre probabilidades, vantagem e variância? Quais são as implicações na banca de probabilidades variáveis? Continue a ler para saber a resposta.
Ao entender o que esperar de uma série de apostas, a boa gestão da banca ajudará o apostador a evitar certos vieses comportamentais, tais como o viés de autoconfiança, o viés de autoatribuição e a ilusão de competência, que podem desgastar a esperada rentabilidade a longo prazo. Este artigo explora como probabilidades, vantagem e variância interagem e podem orientar as expectativas de banca dos apostadores.
Gestão de banca
Gerir a banca e compreender a variância são competências cruciais para qualquer apostador. De jogadores de póquer a apostadores desportivos, as características que todos os apostadores de sucesso devem possuir incluem a capacidade de compreender e quantificar a sua vantagem e de atribuir variância simultaneamente à sorte ou ao azar.
Considere uma aposta com probabilidades de 2,0, que implica uma possibilidade (sem margem) de 50%. Se um apostador puder determinar precisamente que a possibilidade real é 52% (avaliação real de 1,92), o retorno esperado para cada aposta feita a 2,0 será de 4% (2,0/1,92 – 1). Isto pode ser referido como a “vantagem” do apostador.
Agora, vamos supor que um apostador começa com uma banca de 100 unidades e aposta uma unidade fixa. Depois de 100 apostas, a banca do apostador poderá situar-se entre 0 e 200 unidades; contudo, espera-se que seja de 104 unidades – um lucro de 4%.
Se simularmos este cenário 10 000 vezes, podemos ver o efeito da variância na banca do apostador no gráfico abaixo.
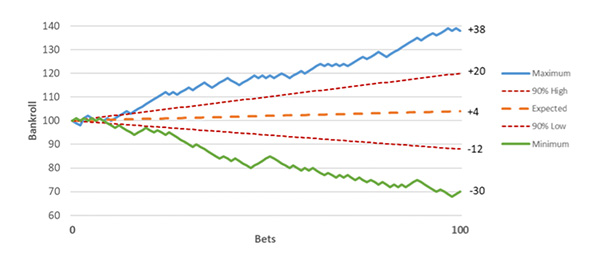
Divida sua banca por no mínimo 100 unidades caso você seja uma pessoa que goste de risco. O número ideal caso você siga mais de 1 tipster, são 200 unidades.
By Pinnacle – JONATHON BRYCKI -
O efeito da “mão quente”: a natureza das sequências de vitórias

Já teve a sensação de estar em uma maré de sorte? Que tudo o que você tocava ou fazia geraria resultados incríveis? Você pode até ter se convencido de que atletas e estrelas do esporte são iguais e que, depois de ganhar algumas vezes, eles têm a certeza de que vencerão novamente. No entanto, as evidências sugerem que o efeito da “mão quente” é exagerado e, principalmente, se trata de uma questão de sorte. Como isso influencia as suas apostas e como você pode incluir isso como um fator nas suas próprias análises?
O que é o efeito da “mão quente”?
O termo mão quente vem do basquete, em que o pensamento predominante era que um jogador capaz de converter vários arremessos consecutivos tem maior probabilidade de marcar no arremesso seguinte. Todos, desde treinadores, fãs e comentaristas até os próprios atletas, ficam convencidos do poder desse efeito. No entanto, vários estudos demonstram que o efeito da “mão quente” tem menos probabilidade de determinar um resultado do que o puro acaso.
Estudos sobre outros esportes, como o beisebol, também demonstraram poucos efeitos da “mão quente” com significância estatística. Ao analisar, desde as sequências de rebatidas às sequências de vitórias das equipes, eventualmente tendemos a notar que estas sequências de vitórias chegam ao fim e as equipes e jogadores retornam ao seu desempenho regular.
Então, se o efeito não existe realmente ou é apenas fraco na melhor das hipóteses, por que damos tanta importância a ele? Parte da razão para isso é evolutiva. Desde os nossos dias como caçadores-coletores, temos sido programados para procurar padrões no nosso ambiente – fontes de alimentos, água e animais tendem a ser agrupados, e isso se reflete nas apostas, quando tentamos garantir que obteremos o máximo de quaisquer tendências que vemos no mercado.
Outra razão é que, porque isso acontece conosco, presumimos que o mesmo ocorre com um atleta altamente capacitado. No entanto, evidências de jogadores de golfe juniores (Cotton e Price, 2006) mostram que, quanto maior o nível de habilidade e experiência de um atleta, menos suscetível ele é aos efeitos da confiança e da crença em si mesmo.
Também temos um viés cognitivo em que sofremos de presentismo, ou a sensação de que as condições atuais durarão mais tempo do que deveriam na realidade.
Exceções ao efeito da “mão quente”
Existem algumas situações em que o efeito da “mão quente” pode fazer alguma diferença:
- Uma análise de dez jogadores de boliche mostrou que eles tinham aproximadamente 12% mais probabilidade de acertar o quinto arremesso se já tivessem acertado outros quatro (Dorsey-Palmateer e Smith, 2004).
- Na competição de tacadas mais difícil da NHL, os estatísticos encontraram uma correlação quase perfeita entre as velocidades de batida dos jogadores (Reifman, 2007).
- Jogadores de tênis tinham maior probabilidade de ganhar seu próximo ponto se tivessem ganho o serviço anterior (Klaasen e Magnus, 2001).
No entanto, todos esses compartilham a característica de serem movimentos repetitivos e com um pequeno intervalo entre as ações. Outras competições baseadas em habilidades, como a competição anual de arremessos de 3 pontos do NBA All Star também podem ser uma dessas exceções, mas o número de variáveis aumenta em competições esportivas (por exemplo, quando há outros jogadores, condições de jogo, o efeito da torcida etc.), como consequência, pode ser mais difícil prever o efeito da “mão quente”.
Como o efeito da “mão quente” influencia suas apostas?
O efeito da “mão quente” pode sugerir que os comentaristas e a mídia influenciam os apostadores casuais no mercado de apostas, destacando jogadores ou equipes em sequências de vitórias incríveis (ou o oposto, com um viés excessivo para a “mão fria”). Os preços das equipes podem ser extremamente exagerados ou subestimados, sugerindo que há valor a ser encontrado em uma abordagem contrária e indo desafiando as tendências atuais.
Estudos nesta área também mostraram que os jogadores ajustam suas estratégias se estiverem conscientes de se encontrarem em uma sequência positiva, e outras equipes podem reagir de forma diferente a esse jogador e reforçar seus esforços para pará-lo, dificultando ainda mais a possibilidade do jogador manter seu desempenho.
Saber quando uma equipe está apresentando um desempenho muito superior ou inferior ao esperado com base na sua própria avaliação objetiva pode ser uma estratégia lucrativa. Atribuir contexto a uma sequência irregular, como os oponentes enfrentados e o estado do jogo, também adicionará outra camada de análise que alguns outros apostadores podem ter ignorado. Isso pode não funcionar sempre mas, como diz o ditado, todas as coisas boas precisam chegar ao fim.
Neel Shah – by Pinnacle -
Como calcular a Distribuição de Poisson?
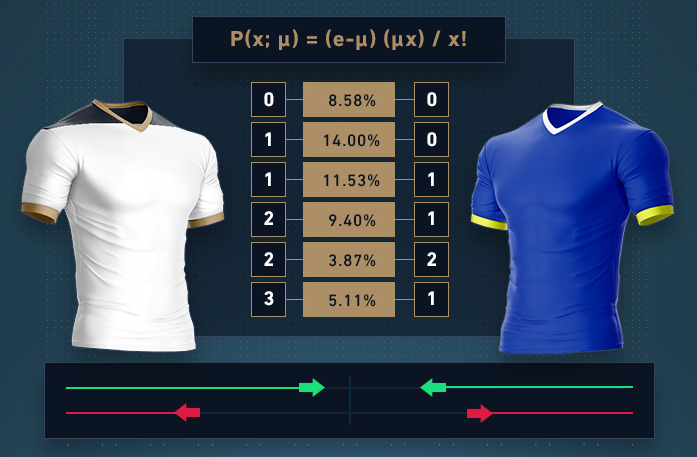
A Distribuição de Poisson, associada aos dados históricos, fornece um método simples e fiável para calcular o resultado mais provável num jogo de futebol que pode ser aplicado às apostas. Esta apresentação simples mostra como calcular as medidas necessárias de capacidade ofensiva/defensiva com um atalho útil para gerar os valores da Distribuição de Poisson. Em pouco tempo, estará a prever os resultados do futebol utilizando a Distribuição de Poisson.
A Distribuição de Poisson é um conceito matemático para converter as médias numa probabilidade para resultados variáveis de uma distribuição. Por exemplo, se soubermos que o Manchester City tem uma média de 1,7 golos por jogo, então ao introduzirmos esta informação numa fórmula da Distribuição de Poisson, veremos que esta média indica que o Manchester City marca 0 golos 18,3% das vezes, 1 golo 31% das vezes, 2 golos 26,4% das vezes e 3 golos 15% das vezes.
Distribuição de Poisson – Calcular as possibilidades dos resultados
Antes de podermos usar a Distribuição de Poisson para calcular o resultado mais provável de um jogo, precisamos de calcular o número médio de golos que é provável que cada equipa marque nesse jogo. Para tal, devemos calcular a capacidade ofensiva e a capacidade defensiva de cada equipa e compará-las.
A seleção de um intervalo de dados representativos é fundamental quando se calcula a capacidade ofensiva e a capacidade defensiva; por um lado, se o intervalo for demasiado grande, os dados não serão relevantes para a capacidade atual das equipas; por outro, se for demasiado curto, pode permitir que valores atípicos enviesem os dados. Os 38 jogos jogados por cada equipa na época de 2015/16 da Premier League inglesa dará uma amostra de tamanho suficiente para aplicar a Distribuição de Poisson.
Como calcular a capacidade ofensiva
O primeiro passo para calcular a capacidade ofensiva com base nos resultados da última época é determinar a média de golos marcados por cada equipa, nos jogos em casa e nos jogos fora.
Para tal, pegamos no número total de golos marcados na última época e dividimos pelo número de jogos disputados:
- Total de golos marcados em casa/número de jogos (na época)
- Total de golos marcados fora/número de jogos (na época)
Na época de 2015/16 da Premier League inglesa, houve 567 golos/380 jogos em casa e 459/380 fora, o que equivale a uma média de 1,492 golos por jogo em casa e 1,207 fora.
- Número médio de golos marcados em casa: 1,492
- Média de golos marcados fora: 1,207
A proporção entre a média da equipa e a média da liga é o que constitui a “capacidade ofensiva”.
Como calcular a capacidade defensiva
Também precisamos da média de golos sofridos por uma equipa média. É simplesmente o inverso dos valores anteriores, uma vez que o número de golos marcados pela equipa da casa é igual ao número de golos sofridos pela equipa visitante:
- Média de golos sofridos em casa: 1,207
- Média de golos sofridos fora: 1,492
A proporção entre a média da equipa e a média da liga é o que constitui a “capacidade defensiva”.
Podemos agora utilizar os números acima para calcular a capacidade ofensiva e a capacidade defensiva tanto do Tottenham Hotspur como do Everton (até 1 de março de 2017).
Prever os golos do Tottenham Hotspur
Calcular a capacidade ofensiva do Tottenham:
- Passo 1: Pegamos no número de golos marcados em casa na última época pela equipa da casa (Tottenham: 35) e dividimos pelo número de jogos em casa (35/19): 1,842.
- Passo 2: Dividimos este valor pela média de golos marcados por jogo pelas equipas da casa (1,842/1,492) para obter uma capacidade ofensiva de 1,235.
(35/19) / (567/380) = 1,235
Calcular a capacidade defensiva do Everton:
- Passo 1: Pegamos no número de golos sofridos fora na última época pela equipa visitante (Everton: 25) e dividimos pelo número de jogos fora (25/19): 1,315.
- Passo 2: Dividimos este valor pela média de golos sofridos por jogo pela equipa visitante na época (1,315/1,492) para obter a “capacidade defensiva” de 0,881.
(25/19) / (567/380) = 0,881
Podemos agora utilizar a fórmula seguinte para calcular o número provável de golos que o Tottenham poderá marcar (para tal, basta multiplicar a capacidade ofensiva do Tottenham pela capacidade defensiva do Everton e pelo número médio de golos marcados em casa na Premier League):
1,235 x 0,881 x 1,492 = 1,623
Prever os golos do Everton
Para calcular o número de golos que o Everton poderá marcar, basta utilizar as fórmulas acima, mas substitua o número médio de golos marcados em casa pelo número médio de golos marcados em jogos fora.
Capacidade ofensiva do Everton:
(24/19) / (459/380) = 1,046
Capacidade defensiva do Tottenham:
(15/19) / (459/380) = 0,653
Da mesma forma que previmos o número de golos que o Tottenham irá marcar, podemos calcular o número provável de golos que o Everton poderá marcar (para tal, basta multiplicar a capacidade ofensiva do Everton pela capacidade defensiva do Tottenham e pelo número médio de golos marcados em jogos fora na Premier League):
1,046 x 0,653 x 1,207 = 0,824
Distribuição de Poisson – prever vários resultados
Claro que nenhum jogo termina com 1,623 ou 0,824 golos – trata-se apenas de uma média. Com a Distribuição de Poisson, uma fórmula criada pelo matemático francês Simeon Denis Poisson, podemos usar estes números para distribuir 100% da probabilidade num intervalo de golos marcados para cada equipa.
Fórmula da Distribuição de Poisson:
P(x; μ) = (e-μ) (μx) / x!

Este exemplo mostra que há 19,73% de hipóteses de o Tottenham não marcar nenhum golo, mas que há 32,02% de hipóteses de marcar um único golo e 25,99% de hipóteses de marcar dois golos. Por outro lado, o Everton tem 43,86% de hipóteses de não marcar nenhum golo, 36,14% de hipóteses de marcar um golo e 14,89% de hipóteses de marcar dois golos. Acha que alguma equipa vai marcar cinco golos? A probabilidade é de 1,85% para o Tottenham ou de 0,14% para o Everton – ou de 2% para qualquer equipa que marque 5.
Uma vez que ambos os resultados são independentes (matematicamente falando), poderá ver que o resultado esperado é de 1-0 – ao emparelhar os resultados mais prováveis para cada equipa. Se multiplicar essas duas probabilidades, obterá a probabilidade de um resultado de 1-0 – (0,3202*0,4386) = 0,1404 ou 14,04%.
Agora que já sabe calcular as possibilidades dos resultados de golos utilizando a Distribuição de Poisson nas apostas, pode comparar as suas medidas com as probabilidades de uma casa de apostas e ver se existem discrepâncias das quais tirar partido, especialmente se levar em consideração na sua própria avaliação os fatores situacionais relevantes, como o clima, lesões ou a HFA.
Converter as hipóteses estimadas em probabilidades
O exemplo acima mostrou-nos que há 11,53% de hipóteses de ocorrer um empate a 1-1 (0,3202*0,3614) quando se aplica a fórmula da Distribuição de Poisson. Mas e se quisesse conhecer as probabilidades previstas no “empate”, em vez de nos resultados individuais do empate? Teria de calcular a probabilidade para todos os empates possíveis, por exemplo, 0-0, 1-1, 2-2, 3-3, 4-4, 5-5, etc.
Para tal, bastaria calcular a probabilidade de todas as combinações de empates possíveis e somá-las. Assim, obteria a probabilidade de se registar um empate, independentemente do resultado.
Naturalmente, existe na realidade um número infinito de possibilidades de empate (por exemplo, ambas as equipas poderiam marcar 10 golos cada), mas as hipóteses de um empate com um resultado acima de 5-5 são tão reduzidas que podemos ignorá-las neste modelo.
Utilizando o exemplo do Tottenham vs. Everton, e combinando todas as possibilidades de empate, dá uma probabilidade de 0,2472 ou 24,72% – tal daria probabilidades reais de 4,05 (1/0,2472).
Os limites da Distribuição de Poisson
A Distribuição de Poisson é um modelo preditivo simples que não permite ter em conta muitos fatores. Este modelo ignora completamente fatores situacionais – como as circunstâncias do clube, a importância do jogo, etc. – e a avaliação subjetiva das mudanças em cada equipa durante o período de transferências.
Neste caso, o cálculo da fórmula de Poisson acima não consegue quantificar o efeito que o novo treinador do Everton (Ronald Koeman) poderia ter tido na equipa. Também não consegue levar em consideração a potencial fadiga do Tottenham agora que estão a jogar próximo a um encontro da Liga Europa.
Além disso, o modelo ignora as correlações, como por exemplo o amplamente reconhecido estado do terreno que afeta a possibilidade de haver muitos ou poucos golos num jogo.
Estes são aspectos particularmente importantes em jogos de ligas de menor importância, que podem dar aos apostadores uma vantagem face às casas de apostas. É mais difícil obter uma vantagem em ligas mais importantes, como a Premier League, considerando a experiência e os recursos que as casas de apostas modernas têm à sua disposição.
Por último, mas não menos importante, estas probabilidades não levam em consideração a margem que uma casa de apostas cobra que é extremamente importante para todo o processo de encontrar valor.
by: Pinnacle. -
Precificação via expected Goals (xG)
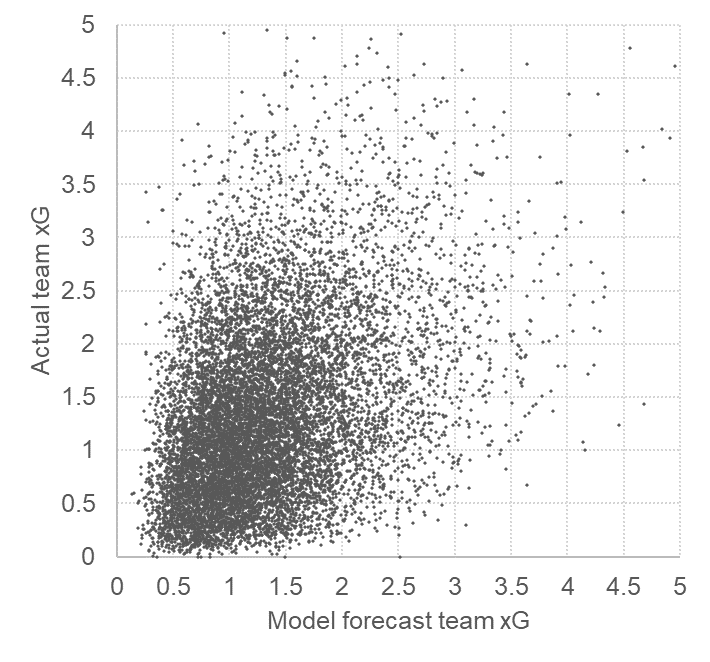
A estatística de expectativa de gols é uma ferramenta de previsão popular. Os apostadores podem usar a expectativa de gols para determinar um resultado com precisão? O analista de apostas Joseph Buchdahl processa dados e determina se a expectativa de gols pode prever resultados de futebol.
As apostas esportivas, pelo menos para aqueles que aspiram a tratá-las como mais do que uma atividade recreacional, estão familiarizadas há algum tempo com o conceito de expectativa e, especificamente, com a ideia de valor esperado.
Apostas podem ser ganhadoras e perdedoras, mas muito do que acontece é meramente uma consequência do acaso.
No entanto, saber o valor esperado de algo, a longo prazo, permite ao apostador ter uma estimativa de quanto pode esperar ganhar ao longo de uma amostra maior de apostas. “Expectativa” é apenas outra palavra para “média aritmética” ou “média”.
Mais recentemente, o conceito de expectativa se fez presente no futebol por meio da noção de expectativa de gols ou xG. A expectativa de gols é usada como uma métrica de desempenho para avaliar um time de futebol ou o desempenho de um jogador através da atribuição de uma probabilidade à oportunidade de marcação que pode resultar em um gol.
Esse cálculo é feito por meio do uso do histórico de dados para oportunidades equivalentes e da taxa de conversão de gol. Portanto, a xG para uma oportunidade de marcação estará entre 1 e 0.
Além disso, somar a xG em um jogo com várias oportunidades de gols resultará na xG para o próprio jogo ou, mais comumente, em uma xG para cada time em um jogo.
Em teoria, a xG fornece uma representação mais verdadeira da qualidade de jogo das equipes em um jogo e da superioridade de uma equipe em relação ao adversário do que os dados dos gols em si.
Os gols são marcados com um nível razoável de acaso (o que os especialistas chamam de “ruído”) e o uso de um placar real para prever o que uma equipe poderá fazer no seu próximo jogo pode ser menos confiável do que usar a xG dessa equipe.
De certa forma, os gols são como vitórias e derrotas em uma aposta, enquanto a expectativa de gols é como o valor esperado. Se for esse o caso, podemos usar a xG ao invés de gols para prever o resultado de partidas de futebol para ganho em apostas?
Gols x Expectativa de gols
David Sumpter, matemático e autor de Soccermatics: Mathematical Adventures in the Beautiful Game, deu um direcionamento sobre a utilidade relativa de gols versus xG quando se tenta prever o resultado de jogos futuros. Sumpter ilustra a dificuldade de encontrar um sinal de previsão a partir dos dados de gols de forma sucinta.
“De um ponto de vista estatístico, o resultado de uma partida de futebol é quase tanto ruído quanto é sinal. Uma explicação matemática para isso pode ser encontrada diretamente na distribuição de Poisson. No futebol, os gols seguem a distribuição de Poisson e as equipes marcam, em média, 1,4 gols. O desvio e a média são iguais na distribuição de Poisson. Sendo assim, o desvio padrão é a raiz quadrada de 1,4, ou seja, 1,18. Consequentemente, o ruído (1,18) é apenas ligeiramente menor do que o sinal (1,4).”
A xG, ao contrário, é uma medida de probabilidades criadas e, assim, proporciona uma medida melhor da qualidade de uma equipe durante um único jogo em comparação ao número de gols.
Normalmente, ela apresenta menor ruído e mais sinal. Tanto para gols quanto para xG, a quantidade de ruído nos resultados das partidas diminui à medida que o número de jogos sendo analisados aumenta. No entanto, o índice de diminuição é inicialmente mais acentuado para a xG do que para os gols.
Sumpter usa essa informação para recomendar qual o tipo de dados que deve ser nosso foco quando tentamos fazer previsões para jogos futuros. Para uma ou duas partidas, é o próprio relatório da partida que fornece as informações mais úteis.
Por outro lado, para amostras superiores a 15 partidas, ou para a melhor parte da metade de uma temporada, os dados de gols serão tão confiáveis quanto as xG.
O ruído ainda será um pouco maior, mas a diferença é menor. Além disso, os gols representam a realidade – o que aconteceu – enquanto a xG é um modelo probabilístico de chances de marcação. Se não for precisa, poderá inclusive ser menos confiável do que os dados de gols.
Entre esses extremos está uma área empolgante da perspectiva de utilização da xG como uma ferramente de previsão. Sumpter argumenta que o relatório da xG será mais útil entre três e seis jogos, enquanto que para sete a 15 partidas será, possivelmente, mais apropriada a comparação entre gols e xG.
Clique aqui para saber como calcular a Distribuição de Poisson!
by Pinnacle.
-
Quais os melhores sites para comparação de odds?!

Abaixo temos uma lista de sites onde você pode comparar odds de um evento esportivo entre casas de aposta!


-
Descomplicando Termos das Apostas Esportivas

Probabilidades (Odds): São as chances de um evento acontecer em um jogo ou campeonato. Elas são representadas por números, como 1,5, 2,0, 4,5, e indicam quanto você pode ganhar com base na sua aposta.
Odds Decimais: É a forma mais comum de odds usada no Brasil, como 1,5 ou 2,0. Para calcular seus ganhos, basta multiplicar sua aposta pelo valor da odd. Por exemplo, se a odd é 1,5 e você aposta R$ 10, seu lucro será de R$ 15 (R$ 10 x 1,5).
Odds Européias: São apresentados em formato de frações, como 9/1 ou 7/3.
Odds Americanas: São representados por números positivos ou negativos, como +260 ou -180.
Moneyline: É a aposta mais popular no futebol, onde você escolhe apenas o vencedor do jogo, sem se preocupar com o placar exato.
Hipótese Dupla: É uma aposta mais segura, onde você escolhe dois dos três possíveis resultados de um jogo, por exemplo, vitória do time da casa ou empate.
Empate Anula a Aposta: Nessa aposta, se o jogo terminar em empate, seu dinheiro é devolvido.
Handicap: É uma forma de equilibrar as cotações, adicionando margens de vantagem ou desvantagem para as equipes.
Ambas as Equipes Marcam Gols: Nessa aposta, você decide se as duas equipes vão marcar gols ou não, independente do resultado final.
Gestão de Banca: É a estratégia de administrar bem o dinheiro disponível para apostas, evitando riscos excessivos.
Cash Out: É a opção de vender sua aposta antes do fim do evento, para minimizar perdas.
Bookmaker: É o termo para casas de apostas.
Conta: É o saldo de recursos em sua conta na casa de apostas, onde você deposita e retira dinheiro.
Depósito: É o dinheiro que você coloca na sua conta para começar a apostar.
Bônus: Valor oferecido pelas casas de apostas para incentivar os usuários a se cadastrarem e apostarem mais.
Rollover: Número mínimo de apostas que você precisa fazer antes de poder sacar o dinheiro obtido com o bônus.
Free Bet: Aposta grátis oferecida por algumas casas de apostas, onde você fica com o lucro caso acerte, e o valor da aposta é devolvido se errar.
Juice: É a porcentagem que a casa de apostas recebe a cada palpite realizado, mantendo o funcionamento do site. Geralmente varia entre 5% e 10%.
Um grupo que vive e respira apostas esportivas. Há três anos encaramos esse universo com dedicação e método, buscando sempre formas de melhorar e gerar resultados consistentes para quem acompanha nosso trabalho.
